Functii recursive in JavaScript
Recursivitate cu bune si rele

Functii recursive in JavaScript
Despre recursivitate
Mai intai de toate sa stabilim ca toti stim ce inseamna o functie recursiva: o functie care contine cod ce apeleaza chiar functia respectiva. Deci o functie care se auto-apeleaza.
Este obligatoriu sa avem o limita, o conditie de stop, altfel putem ajunge la cicluri infinite ce se lasa cu blocarea aplicatiei.
Cand putem folosi recursivitatea? In general, daca avem un calcul care se poate separa intr-o serie de calcule similare, atunci putem aplica recursivitatea. De multe ori delegam (incapsulam) sub-taskuri catre alte functii. Un caz particular este cand putem delega chiar catre functia curenta.
Daca aveti in codul vostru un for, while, do while, etc..., sunt sanse mari sa-l puteti rescrie folosind o functie recursiva. Este foarte util in sortari si traversarea structurilor de date complexe (un tree de exemplu).
De ce am face asta? Codul recursiv este, de obicei, mult mai succint. Totodata simplificam mentenanta variabilelor locale. Aceeasi functie executata repetitiv are propriul context. De exemplu, daca pe stack avem: fn(a) -> fn(a) -> fn(a), atunci sunt 3 variabile locale a care nu se vor incurca intre ele.
Un cod succint nu inseamna si ca va fi mai eficient. Codul echivalent, folosind bucle (for, while, etc.) va fi probabil mai rapid. Insa de multe ori nu este o diferenta care sa conteze si atunci simplitatea codului primeaza.
Un exemplu simplu
Sa consideram ca JavaScript nu stie sa faca inmultiri. Va fi destul de greu sa ne inchipuim asta, poate ca ar fi trebuit sa iau alt exemplu. Ca sa va asigurati ca JavaScript stie sa faca inmultiri puteti sa verificati codul urmator in consola din browser:
console.log( 1.1 * 1.1 )
Hm… am verificat si eu, cred ca am ales exemplul gresit, insa la inmultirea cu numere intregi nu are nicio problema…
Deci, sa implementam un algoritm care sa ne ofere rezultatul inmultirii intre doua numere, folosind doar operatia de adunare:
3 x 4 = 3 + 3 + 3 + 3 = 12
function inmulteste(a, b) {
// nu acceptam decat un b pozitiv (recursivitatea se termina)
if (!b || b < 0) return false;
// cazul de baza (deasemenea termina recursivitatea dar cu succes)
if (b === 0) return 0; // a * 0 = 0
console.log(`In acest pas am de adunat ${a} la rezultatul lui inmulteste(${a},${b-1}), adica ${a*(b-1)}`);
console.log(`Voi returna apelantului ${a+a*(b-1)}`);
return a + inmulteste(a, b - 1);
}
inmulteste(3,4); // 12
Mai jos este rezultatul in consola:
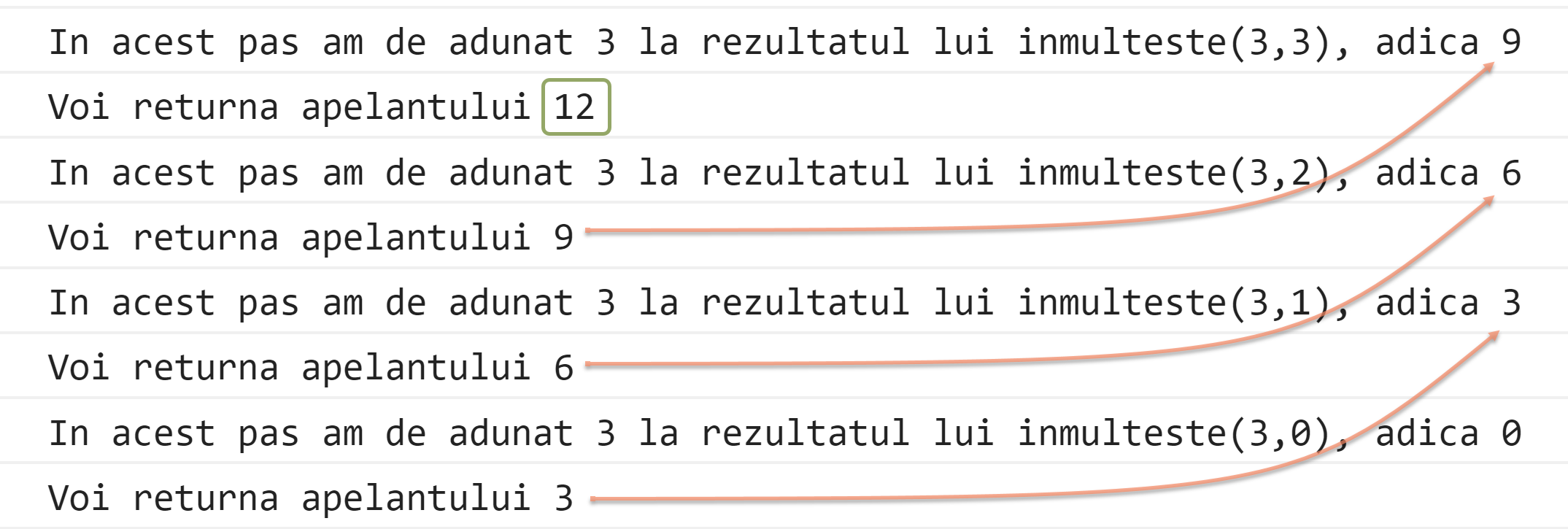
Trei elemente care ar fi bine sa fie prezente la o functie recursiva
1. Conditia de SUCCESS STOP
Vorbim aici de cazul de baza. Daca am ajuns la el recursivitatea s-a incheiat cu succes.
if (b === 0) return 0;
Conditia de STOP SUCCESS este invocata in cel mai de sus apel pe stiva (thread-ul aplicatiei). La baza stivei este apelul inmulteste(3,4):
inmulteste(3,4) -> inmulteste(3,3) -> inmulteste(3,2) -> inmulteste(3,1) -> inmulteste(3,0);

Din stack ne putem da seama ca recursivitatea poate fi mai ineficienta in comparatie cu un loop. Cu cat avem mai multe imbricari, cu atat stiva este mai plina, si fiecare functie de pe stiva trebuie sa-si mentina contextul (variabilele locale).
2. Conditia de ERROR STOP
Orice erori, parametri lipsa, cazuri neasteptate trebuie sa fie prinse si sa opreasca recursivitatea.
if (!b || b < 0) return false;
3. Apelarea recursiva
Functia se cheama pe ea insasi:
inmulteste(a, b - 1);
Observam si din Call Stack ca de fapt recursivitatea este o serie de functii imbricate. Functia de pe nivelul cel mai adanc va fi prima care returneaza o valoare. Celelalte vor returna pe rand in ordinea inversa apelarii.
Calcularea factorialului
Un alt exemplu clasic unde putem utiliza functii recursive ar fi calcularea factorialului unui numar. Este foarte similar cu exemplul anterior:
// n! - apelare recursiva pentru n * (n-1) * (n-2) ...
function factorial(n) {
if (n < 0) return false;
// daca am ajuns la 0 nu returnam 0 pentru ca ne anuleaza tot calculul
// returnam 1 care nu influenteaza inmultirea
// totodata semnalizam si incheierea cu success a recursivitatii
if (n === 0) return 1; // conditia de SUCCESS STOP
return n * factorial(n - 1);
}
factorial(4); // 4 * 3 * 2 * 1
Schema recursiva este:
factorial(3) > 3 * factorial(2) > 2 * factorial(1) > 2 * factorial(0)
Inversarea unui text
Putem utiliza functii recursive ca sa modificam un text in txet. Foarte utila functie, mai ales in cazul acestui exemplu.
Inainte sa implementam versiunea recursiva, sa vedem cum am putea fi mai eficienti in inversarea unui text:
In JavaScript exista functia reverse() dar nu pentru string-uri, ci pentru array-uri.
console.log( "text".split().reverse().join() )
Asta a fost usor. Acum sa trecem la varianta recursiva.
function textInvers(text){
if (text === '') return '';
if (!text) return false; // !text prinde si sirul vid, de-asta SUCCES STOP e primul
// "text".substr(1) = "ext"
console.log(text.substr(1), text[0]);
return textInvers(text.substr(1)) + text[0]; // sau text.charAt(0)
}
textInvers('text'); // 'txet'
Schema executiei. Nu uitam ca cea mai imbricata functie returneaza prima (adica conditia de SUCCESS STOP):
textInvers('text') > textInvers('ext') + 't' > textInvers('xt') + 'e' > textInvers('t') + 'x' > textInvers('') + 't'
In ordine inversa avem valorile returnate din functiile apelate recursiv:
'' + 't' = t > 't' + 'x' = tx > 'tx' + 'e' = txe > 'txe' + 't' = txet > 'txet'
Ridicarea la putere
Este o functie similara cu cele de mai sus.
Mai intai varianta cu for:
function x_LaPuterea_n(x, n) {
var rez = 1;
for (var i = 0; i < n; i++) {
rez *= x; // rez = rez * x
}
return rez;
}
Varianta recursiva:
function x_LaPuterea_n(x, n) {
// if (n == 1) return x; // SUCCESS STOP 1
if ( n !== undefined && n === 0) return 1; // 0^0 = 1
// aici nu mai poate fi n = 0, a iesit mai sus
// cazul particular 0^0 este tratat deja, acum avem 0^orice = 0
if ( x !== undefined && x === 0 ) return 0; // SUCCESS STOP 2
if (!x || !n) return false; // ERROR STOP
return x * x_LaPuterea_n(x, n - 1);
}
console.log( x_LaPuterea_n(0,0) ); // 1
console.log( x_LaPuterea_n(2,0) ); // 1
console.log( x_LaPuterea_n(0,2) ); // 0
console.log( x_LaPuterea_n(2,2) ); // 4
Din cauza cazurilor particulare, la ridicarea la putere am avut doua cazuri de iesire pe ‘SUCCESS STOP’
Structuri complexe de tip arbori
Sa presupunem ca avem urmatoarele date:
var puncteDeLucru = {
constanta: [
{ name: 'Andrei', points: 10 },
{ name: 'Alice', points: 16 }
],
bucuresti: {
sector1: [
{ name: 'Marian', points: 20 },
{ name: 'Mihai', points: 18 }
],
sector2: [
{ name: 'Ana', points: 14 }
]
}
};
Datele sunt organizate sub forma regiune -> subregiune -> subregiune ....
Practic am putea sa cream oricate imbricari daca este nevoie sa impartim o regiune/subregiune in mai multe felii.
Pentru inceput, sa incercam sa traversam intreaga structura folosind recursivitatea. Nu avem de unde sa stim cate nivele de imbricare avem, asa ca pare un caz potrivit pentru recursivitate.
Sa observam datele:
-
In momentul cand intalnim un array, vorbim de frunze, adica de ultimul nivel al ramurii
-
In momentul cand intalnim un obiect, fiecare proprietate a obiectului este o subregiune
Frunzele sunt conditii de SUCCESS STOP iar peste proprietatile obiectului aplicam recursivitatea.
function traversareArbore(regiune) {
if (Array.isArray(regiune)) { // `SUCCESS STOP`
console.log(`SUCCESS STOP`, JSON.stringify(regiune) );
return regiune;
}
console.log('Subtree: ', JSON.stringify(regiune) );
// Recursivitate
for (var subregiune of Object.values(regiune)) {
traversareArbore(subregiune); // chemam recursiv sub-regiunile
}
}
traversareArbore(puncteDeLucru)
Traversarea completa a arborelui in consola:
Subtree: {
"constanta":[...],
"bucuresti":{
"sector1":[...],
"sector2":[...]
}
}
SUCCESS STOP [{"name":"Andrei","points":10},{"name":"Alice","points":16}]
Subtree: {
"sector1":[...],
"sector2":[...]
}
SUCCESS STOP [{"name":"Marian","points":20},{"name":"Mihai","points":18}]
SUCCESS STOP [{"name":"Ana","points":14}]
Mai departe am vrea sa calculam punctajul total. Putem combina recursivitatea cu reduce():
function totalPuncte(regiune) {
if (Array.isArray(regiune)) { // `SUCCESS STOP`
// adunam puncatjul de pe array
return regiune.reduce( (acc, current) => acc + current.points, 0);
}
var total = 0;
// Recursivitate
for (var subregiune of Object.values(regiune)) {
total += totalPuncte(subregiune); // chemam recursiv sub-regiunile
}
return total
}
totalPuncte(puncteDeLucru); // 78
Sa complicam putin problema. Am vrea sa obtinem agregari pentru toate ramurile: suma pentru constanta, suma pentru bucuresti dar si suma pentru sector1 si sector2. Toate astea le vrem la final pe un obiect.
Avem mai jos o solutie recursiva.
Observam ca am folosit o conventie pentru return: un array de forma [total, obiect agregari]
function toateSumele(regiune) {
// array - sunt frunze
if (Array.isArray(regiune)) { // `SUCCESS STOP`
// adunam punctajul de pe array - il returnam sub forma [ total, undefined ]
return [ regiune.reduce( (acc, current) => acc + current.points, 0), undefined ];
}
var total = 0; var gData = {};
// Recursivitate - daca suntem aici inseamna ca avem subregiuni (este obiect)
for (var regProperty of Object.keys(regiune)) {
var recResponse = toateSumele(regiune[regProperty]); // chemam recursiv sub-regiunile
// Object.assign va imbunatati obiectul gData cu noi proprietati
// { [regProperty]: recResponse[0] } = { constanta: 26 }
Object.assign( gData, recResponse[1], { [regProperty]: recResponse[0] } );
total += recResponse[0]; // totalul pe regiune sau subregiune obtinut recursiv
}
// pe masura ce ne vine rezultatul pe cate o regiune o returnam apelantului
return [ total, gData ]
}
var agregari = toateSumele(puncteDeLucru);
console.log( agregari );
Cum ar arata ordinea in care se fac calculele sumelor:
CALCUL FRUNZE 26
APELARE RECURSIVA pentru constanta [26,null]
CALCUL FRUNZE 38
APELARE RECURSIVA pentru sector1 [38,null]
CALCUL FRUNZE 14
APELARE RECURSIVA pentru sector2 [14,null]
RETURNAM CALCUL REGIUNE [52,{"sector1":38,"sector2":14}]
APELARE RECURSIVA pentru bucuresti [52,{"sector1":38,"sector2":14}]
RETURNAM CALCUL REGIUNE [78,{"constanta":26,"sector1":38,"sector2":14,"bucuresti":52}]
Observam ca avem calculate prima data frunzele apoi se returneaza valorile sus in arbore catre root.
Structura de tip tree din date aflate in relatii parent-child
Practic avem un set de date, un array de obiecte, si fiecare obiect are un camp parentid.
Prin conventie putem stabili ca root-ul tree-ului are id-ul 0 sau null.
var treeData = [
{id: 1, department: 'A', parentid: 0},
{id: 2, department: 'B', parentid: 0},
{id: 3, department: 'A1', parentid: 1},
{id: 4, department: 'A1a', parentid: 3},
{id: 5, department: 'A1a1', parentid: 4},
{id: 6, department: 'A1a2', parentid: 4},
{id: 7, department: 'A1b', parentid: 3},
{id: 8, department: 'B1', parentid: 2}
]
Pentru inceput vom parcurge intregul tree pornind de la root (dam parametrul parentid = 0):
function parcurgereTree(arr, parentid) {
for(var i in arr) {
// cautam toate obiectele copil pornind de la parentid = 0
if(arr[i].parentid == parentid) {
console.log(arr[i]);
parcurgereTree(arr, arr[i].id)
}
}
}
parcurgereTree(treeData, 0);
Raspunsul in consola este:
{id: 1, department: "A", parentid: 0}
{id: 3, department: "A1", parentid: 1}
{id: 4, department: "A1a", parentid: 3}
{id: 5, department: "A1a1", parentid: 4}
{id: 6, department: "A1a2", parentid: 4}
{id: 7, department: "A1b", parentid: 3}
{id: 2, department: "B", parentid: 0}
{id: 8, department: "B1", parentid: 2}
Complicam putin problema si acum vrem sa obtinem o structura de date ca mai jos:
[
{ department: 'A',
children: [
{department: 'A1',
children: [
{department: 'A1a',
children: [
{department: 'A1a1'},
{department: 'A1a2'}
]},
{department: 'A1b'}
]}
]},
{department: 'B',
children: [
{department: 'B1'}
]}
]
Vom modifica codul de mai sus ca sa putem construi si returna aceasta transformare:
function convertToTree(arr, parentid) {
let newDataStructure = [];
for(let i in arr) {
// cautem toate obiectele copil pornind de la parentid = 0
if(arr[i].parentid == parentid) {
// vom returna recursiv array-ul cu obiectele copil ale parintelui curent
let listaCopii = convertToTree(arr, arr[i].id)
// daca exista copii atunci ii atasam unei noi proprietati pe parinte
if (listaCopii && listaCopii.length) {
arr[i].children = listaCopii
}
newDataStructure.push(arr[i])
}
}
return newDataStructure;
}
var depTree = convertToTree(treeData, 0);
Am obtinut o noua structura de date. Dupa caz e posibil sa ne fie mai usor sa o utilizam in aplicatia noastra:
[
{
"id": 1, "department": "A", "parentid": 0,
"children": [
{
"id": 3, "department": "A1", "parentid": 1,
"children": [
{
"id": 4, "department": "A1a", "parentid": 3,
"children": [
{ "id": 5, "department": "A1a1", "parentid": 4 },
{ "id": 6, "department": "A1a2", "parentid": 4 }
]
},
{ "id": 7, "department": "A1b", "parentid": 3 }
]
}
]
},
{
"id": 2, "department": "B", "parentid": 0,
"children": [
{ "id": 8, "department": "B1", "parentid": 2 }
]
}
]
Tail Code Optimization
Cand discutam despre functii recursive, putem intalni termenul de Tail Code Optimization. Asta tine mai putin de noi, ca developeri, si mai mult de limbajele de programare si compilatoarele lor. Este o optimizare gandita pentru apelurile recursive. Practic, in loc sa se cumuleze pe stiva toate apelurile recursive, compilatorul va returna imediat valorile din ciclul curent fara sa se umple memoria cu intregul lant de referinte recursive.
JavaScript nu are implementata aceasta optimizare, desi exista ca propunere in specificatiile ECMAScript.




Share this post
Twitter
Google+
Facebook
Reddit
LinkedIn
StumbleUpon
Pinterest
Email